Venn Diagrams Explanations

Venn Diagrams
Venn diagrams are part of the assessment that many people struggle with. You have to teach yourself to look at each question in the same way and not to rely too much on your feelings. Many assignments are designed to mislead you, so if you only rely on your feelings, you will make mistakes. Below is an example where you cannot rely on your feelings.
Which figure best represents the relationship between the following three collections?
- Pancakes
- Syrup
- Syrup Bottles
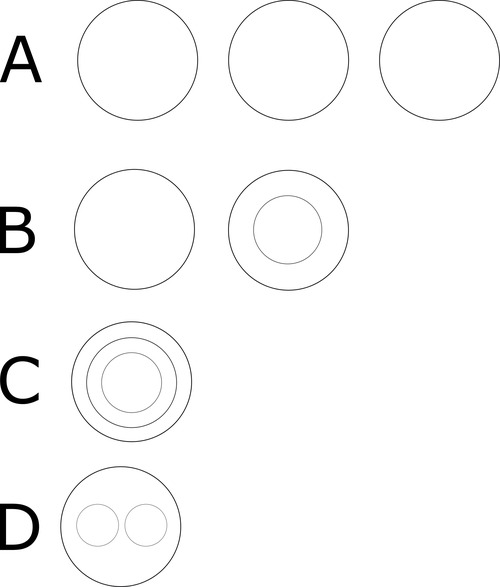
You might think, you can put syrup in a syrup bottle and use the syrup bottle to put the syrup on your pancake. However, this does not lead you to the correct answer. The question is always whether there is an overlap between the collections.
Therefore always ask yourself:
- Can syrup sometimes, always or never be a pancake? And vice versa?
- Can syrup sometimes, always or never be a syrup bottle? And vice versa?
- Can a syrup bottle always or never be a pancake? And vice versa?
All these questions are answered with “never” in this case, so the correct answer must be A. The collections are completely separate from each other.

In the exercises you receive on your assessment, there are 11 possible ways to represent the relation between 3 collections. Below we give an example for each possibility.
- The three collections are completely separate from each other.

An example of three collections that can best be represented as this:
- Vacationers
- Airplanes
- Plane tickets
- Can a Vacationer sometimes, always or never be an airplane? And vice versa? ⇒ never
- Can a Vacationer sometimes, always or never be an airplane? And vice versa? ⇒ never
- Can an airplane sometimes, always or never be a plane ticket? And vice versa? ⇒ never
There is no possible overlap between the collections, so they should not overlap in the figure.
- A collection completely separate, another collection completely within another collection.
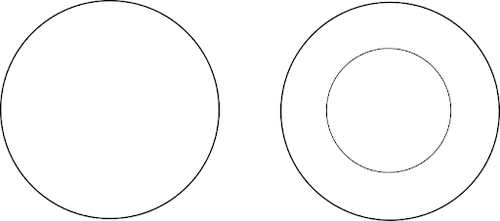
An example of three collections that can best be represented as follows:
- Taxis
- Means of transport
- Taxi drivers
- Can a taxi sometimes, always or never be a means of transport? And vice versa? ⇒ always; and vice versa, a means of transport is sometimes a taxi.
- Can a taxi sometimes, always or never be a taxi driver? And vice versa? ⇒ never
- Can a means of transport sometimes, always or never be a taxi driver? And vice versa? ⇒ never
A taxi is always a means of transport and a means of transport is sometimes a taxi. This is therefore represented by a smaller circle (the taxis) in a larger circle (the means of transport).
The taxi drivers do not overlap with the other collections, so they should be shown separately.
- Two collections overlap and a third collection falls entirely within the other two collections.
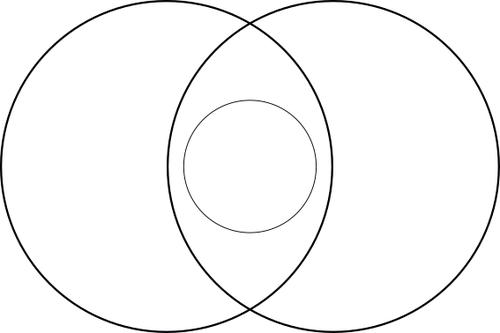
An example of three collections that can best be represented like this:
- Birds
- Black animals
- Adult crows
- Can a bird sometimes, always or never be a black animal? And vice versa? ⇒ A bird is sometimes a black animal; and vice versa, a black animal is sometimes also a bird. (think of black panthers and yellow canaries etc.)
- Can a bird sometimes, always or never be an adult crow? And vice versa? ⇒ a bird is sometimes an adult crow (that canary again); and vice versa an adult crow is always a bird.
- Can a black animal be an adult crow, always or never? And vice versa? ⇒ sometimes (that panther again); and vice versa an adult crow is always a black animal.
So you can see that the collection of crows must fall completely within the other collections and that the collection of birds and black animals overlap with each other, but also have parts where they don’t overlap.
4) Two collections partly overlap and completely fall within a third collection.
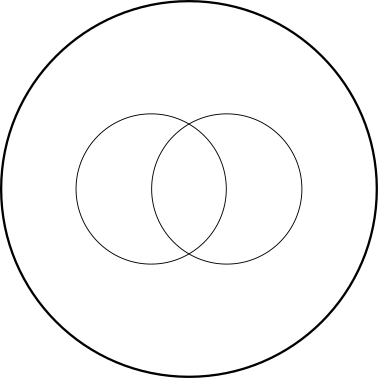
An example of three collections that can best be represented like this:
- Sweet dogs
- Labradors
- Animals
- Can a sweet dog sometimes, always or never be a labrador? And vice versa? ⇒ A sweet dog is sometimes a labrador; and vice versa a labrador is sometimes also a sweet dog. (think false labradors)
- Can a sweet dog sometimes, always or never be an animal? And vice versa? ⇒ a sweet dog is always an animal and vice versa, an animal is sometimes a sweet dog.
- Can a labrador be an animal, always or never? And vice versa? ⇒ a labrador is always an animal and vice versa an animal is sometimes a labrador.
You see that labradors and sweet dogs partly overlap and partly do not. But naughty labradors, sweet labradors (the part that overlaps with sweet dogs) and all other sweet dogs are completely within the collection of animals.
5) A collection falls entirely within another collection, which falls entirely within another collection.
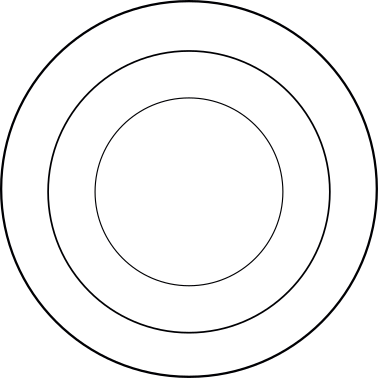
An example of three collections that can best be displayed like this:
- Dogs
- Labradors
- Animals
- Can a dog sometimes, always or never be a labrador? And vice versa? ⇒ A dog is sometimes a labrador; and vice versa a labrador is always a dog.
- Can a dog sometimes, always or never be an animal? And vice versa? ⇒ a dog is always an animal and vice versa an animal is sometimes a dog.
- Can a labrador sometimes, always or never be an animal? And vice versa? ⇒ a labrador is always an animal and vice versa an animal is sometimes a labrador.
You can see that the collection of labradors is completely within the collection of dogs and that the collection of dogs is completely within the collection of animals.
6) Two collections are completely separate, but both fall within a third collection.
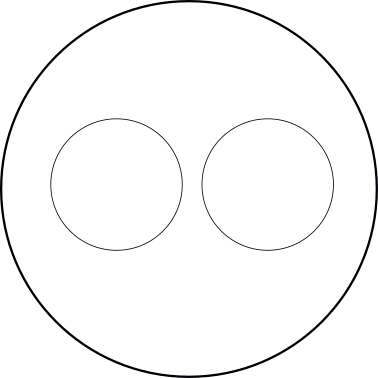
- Dogs
- Cats
- Animals
- Can a dog sometimes, always or never be a cat? And vice versa? ⇒ A dog is never a cat; and vice versa a cat is never a dog.
- Can a dog sometimes, always or never be an animal? And vice versa? ⇒ a dog is always an animal and vice versa an animal is sometimes a dog.
- Can a cat sometimes, always or never be an animal? And vice versa? ⇒ a cat is always an animal and vice versa an animal is sometimes a cat.
You can see that the collection of cats is completely separate from the collection of dogs, but that both collections are completely within the collection of animals.
7) A collection overlaps with two other collections, which in turn are completely separate
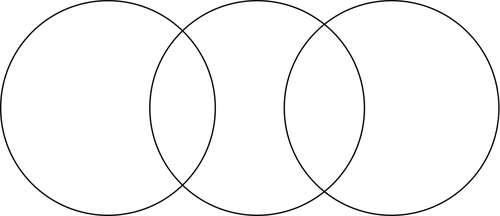
- Dogs
- Cats
- Sweet animals
- Can a dog sometimes, always or never be a cat? And vice versa? ⇒ A dog is never a cat; and vice versa a cat is never a dog.
- Can a dog sometimes, always or never be a sweet animal? And vice versa? ⇒ a dog is sometimes a sweet animal and vice versa, a sweet animal is sometimes a dog.
- Can a cat sometimes, always or never be a sweet animal? And vice versa? ⇒ a cat is sometimes a sweet animal and vice versa, a sweet animal is sometimes a cat.
You can see that the collection of cats is completely separate from the collection of dogs, but that both collections overlap with the collection of sweet animals. However, they don't fall in the collection completely, because there are also naughty cats and dogs.
8) A collection falls entirely within a second collection. A third collection overlaps with the second collection and is completely separate from the first collection
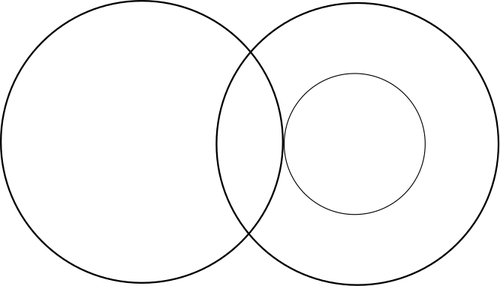
- Sweet dogs
- Cats
- Sweet animals
- Can a sweet dog sometimes, always or never be a cat? And vice versa? ⇒ A sweet dog is never a cat; and vice versa a cat is never a sweet dog.
- Can a sweet dog sometimes, always or never be a sweet animal? And vice versa? ⇒ a sweet dog is always a sweet animal and vice versa, a sweet animal is sometimes a sweet dog.
- Can a cat sometimes, always or never be a sweet animal? And vice versa? ⇒ a cat is sometimes a sweet animal and vice versa, a sweet animal is sometimes a cat.
You can see that the collection of cats is completely separate from the collection of sweet dogs, but overlaps with the collection of sweet animals. The collection of sweet dogs falls entirely within the collection of sweet animals.
9) Three collections all overlap
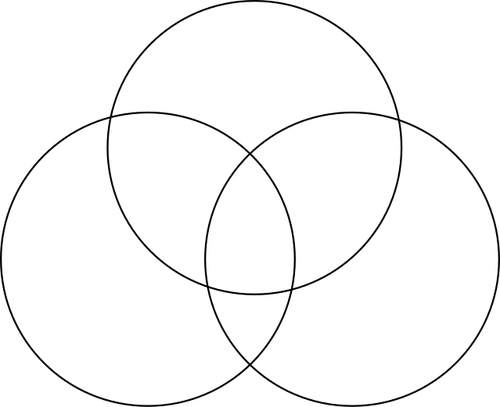
- Sweet dogs
- Puppies
- Labradors
- Can a sweet dog sometimes, always or never be a puppy? And vice versa? ⇒ A sweet dog is sometimes a puppy; and vice versa a puppy is sometimes a sweet dog.
- Can a sweet dog sometimes, always or never be a labrador? And vice versa? ⇒ a sweet dog is sometimes a labrador and vice versa, a labrador is sometimes a sweet dog.
- Can a puppy sometimes, always or never be a labrador? And vice versa? ⇒ a puppy is sometimes a labrador and vice versa, a labrador is sometimes a puppy.
You can see that the collections can all be each other, but also cannot be each other. The piece where they all overlap are the sweet labrador puppies :)
10) Two collections overlap with each other and are completely separate from a third collection
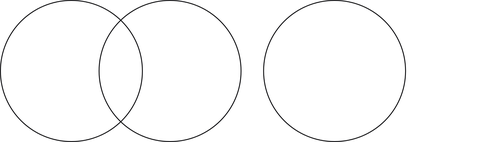
- Sweet dogs
- Puppies
- Cats
- Can a sweet dog sometimes, always or never be a puppy? And vice versa? ⇒ A sweet dog is sometimes a puppy; and vice versa a puppy is sometimes a sweet dog.
- Can a sweet dog sometimes, always or never be a cat? And vice versa? ⇒ a sweet dog is never a cat and vice versa, a cat is never a sweet dog.
- Can a puppy sometimes, always or never be a cat? And vice versa? ⇒ a puppy is never a cat and vice versa, a cat is never a puppy.
You can see that the collections of puppies and sweet dogs overlap with each other, but they cannot be each other. Both collections are completely separate from the collection of cats.
11) Two collections overlap with each other and a third collection falls entirely within one of the collections and partly in the other collection
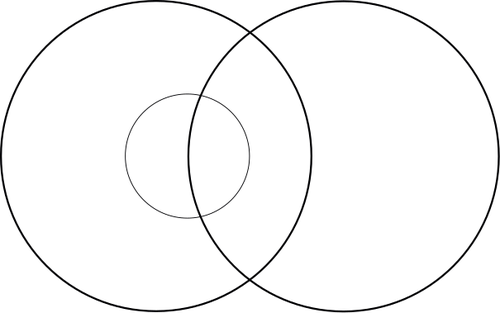
- Sweet dogs
- Labradors
- Labrador puppies
- Can a sweet dog sometimes, always or never be a labrador? And vice versa? ⇒ A sweet dog is sometimes a labrador; and vice versa a labrador is sometimes a sweet dog.
- Can a sweet dog sometimes, always or never be a labrador puppy? And vice versa? ⇒ a sweet dog is sometimes a labrador puppy and conversely a labrador puppy is sometimes a sweet dog.
- Can a labrador sometimes, always or never be a labrador puppy? And vice versa? ⇒ a labrador is sometimes a labrador puppy and conversely a labrador puppy is always a labrador.
You can see that the collection of labrador puppies falls entirely within the collection of labradors and partly overlaps with the collection of sweet dogs (think of the naughty labrador puppies). The collection of labradors has an overlap with the collection of sweet dogs. (think naughty labradors and sweet dachshunds on the other hand).